The rabbit hole, part 2 of who knows how many as it turns out
We're just gonna post whenever we have more, hopefully we won't ultimately abandon this project but we'll see
Part one is over here in case you missed it. The chapters were:
How did we end up so far down the rabbit hole ?
Does physics model everything ?
Are all senses spectral ?
Do the apices of the color spectrum represent a sequence of inverse square roots ?
Moving right along to the next chaptdog.
Does it make any sense to ask how many dimensions the universe is ?
Let’s not sleep on the ramifications if each pure color in the spectrum corresponds to a different number of dimensions, even if we might have made that up. It might inspire us to ask, wait, so how many dimensions is the universe then ? But even as we formulate that question, a dissonance creeps in, and ultimately overwhelms. If each color corresponds to a different number of dimensions, does it even make sense to ask how many dimensions the universe is ? Like, maybe it varies, depending on the situation, or at least depending on the background color.
Let’s revisit the series we derived for mapping wavelength ratios to color spectrum apices — 1/√n, where n is an integer representing a number of dimensions ranging from 3 to 9:
3 dimensions — 1/√3 ratio — red
4 — 1/2 — yellow
5 — 1/√5 — green
6 — 1/√6 — blue
7 — 1/√7 — indigo
8 — 1/√8 — light violet
9 — 1/3 — deep violet
We stumbled upon this series by evenly distributing a vector of fixed length in n dimensions, then measuring the component length in any one dimension.
As it turns out, however, this series has a cameo in a related scene that may be even more applicable, given it actually has to do with wavelengths. And, well, pyramids.
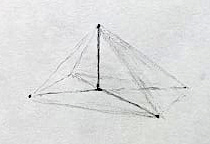
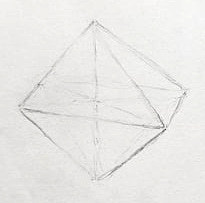
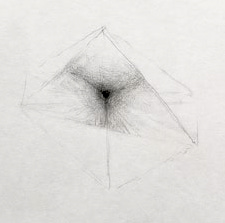
You know the shape of the ancient Egyptian pyramids ? Square bottom, pointy top ? Take that shape, make sure it’s symmetric, and also that the height matches the distance from the center of the base to the corners.
Then, mirror it underneath. It’s basically three axes now, six protrusions, all equal in length, covered by eight stone faces — like a D8 from DnD.
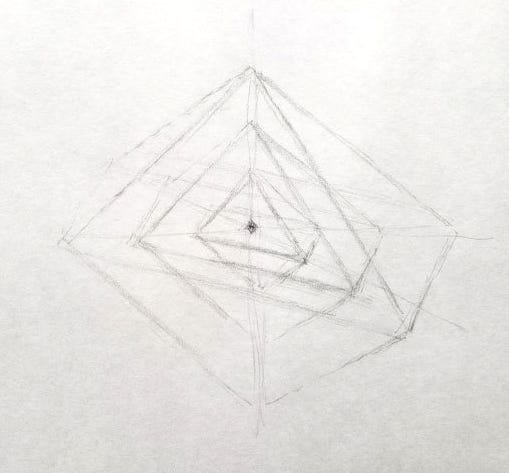
Now go beyond the real world and consider the sort of hyperpyramid that forms as we add more axes, same length, each in a new dimension. At this point we can’t really picture it, we just have to trust the math.
How far away is the surface of the pyramid from the center ?
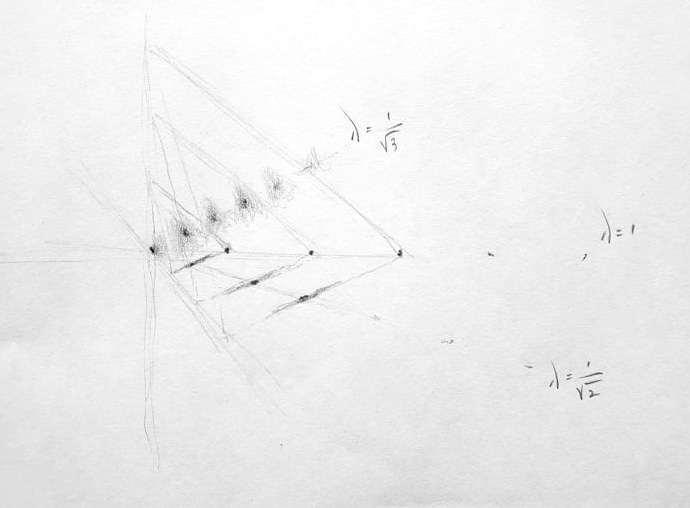
Take it one dimension at a time. If the length of each protrusion is 1, then way back in the first dimension, which might be a little weird to think about, the surface of the “pyramid” is just the tips of opposing protrusions, so that’s easy, the distance is 1.
Second dimension gives us the original bottom square, which is also 1 — at the furthest — but it graduates to a shortest distance in the middle of each side, which happens to be 1/√2.
In three dimensions, we have the same sort of effect — 1 at the furthest (the corners), “nodes” at 1/√2 (the middle of each edge), ultimately graduating to a shortest distance in the “middle” of each triangle face, 1/√3 away from the center.
And from there it continues. So all of a sudden here’s our sequence again — 1/√n, in n dimensions. Indeed, the shortest distance from the center of our pyramid to its surface in n dimensions is 1/√n.
So what’s the significance now ?
We can liken our pyramid to “waves approaching a point,” where a facet of the surface is a flat wavefront and the center of the whole thing is the point. In fact, imagine a series of enclosing pyramids, evenly spaced and shrinking at a steady rate, each disappearing into the point at the center — that’s sort of what we’re getting at.
It might be hard to envision flat waves north of three dimensions — they would indeed have volume — but suffice it to consider this question:
On how many axes are approaching waves balanced ?
If waves approach balanced on n axes, and we scale the wavelength measured along those axes to 1, then the true wavelength is given by 1/√n. That is because the direction of wave propagation is positionally balanced between the n axes — exactly where the shortest distance between waves is.
This phenomenon is very much akin to our pyramid scheme (not that kind). The measurement of 1 taken along the axes is longer than the true wavelength because it is askew to the arriving waves, at least when the waves approach on more than one axis.
We may be wondering at this point how do waves decide to approach on the correct number of axes ? Like, by what mechanism is this achieved ? It would seem a rather tenuous and prohibitively acrobatic maneuver for waves to align with the landing strip and pull in safely, all while traveling at the speed of light, no less. As such, there’s probably another explanation.
The idea would be that it works in reverse — the incoming waves are met naturally by the proper reference frame for their wavelength. We suspect there are no structural axes, after all, but rather a mechanism that conscripts a pseudo frame instantaneously. It could be that the receiver emits its own waves, radiating a series of expanding spheres, interfering with flat passing waves so as to give the interaction its properties — including an effective reference frame. And the orientation of the receiver would have no bearing in this case, assuming its radiation is uniform, which would obviously be convenient. The overarching suggestion is that dimensionality is not a static, preordained property of the universe, but rather varies by interaction, or so would be the leap.
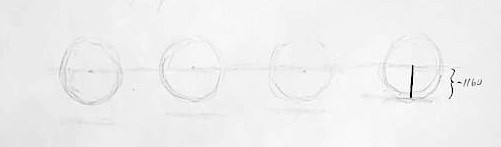
Let’s apply these concepts very loosely to our theoretical basis for the color spectrum. The “calibration” of our color-sensing receiver — which might be the separation between its radiating spheres, else whatever the true mechanism implies — would be ~1160 nm. This would also be — reverting to the archaic notion of a static reference frame — the target wavelength to measure along the receiver’s fixed axes. Now as we’ve been saying, there is no real, rigid, structural frame, but we can superimpose an imaginary one over our spherical receiver for mathematical purposes.
The imaginary frame that overlays the receiver will fluidly pivot on the center point, like the many-faceted answer key inside a Magic 8-Ball, except instead of turning one answer face up it will extend its axes to embrace incoming wavefronts. The number of extended axes will notably vary as separation between wavefronts does — that’s exactly why we have different colors (we guess). This will happen naturally, for the objective is to at all times maximize the number of “calibration axes,” or equally askew axes along which wavelengths measure the calibration of ~1160 nm. Put another way, the frame of the receiver will continuously adjust such that wavelengths stretch to precisely ~1160 nm along as many of its axes as possible.
In moments of perfect balance, there will be some integral number of calibration axes — 3, 4, 5, and so on — while all other axes remain orthogonal to the interaction. These moments will be sensed as pure colors. In stretches of imbalance, there will be some number of calibration axes plus one additional “transition axis” — an axis that measures a wavelength on a trajectory from infinity down to the calibration. These stretches will be sensed as a spectral mix of two colors (or one fading color on the ends of the spectrum).
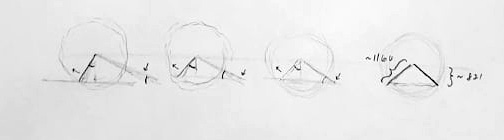
Let’s run the experiment. Start at a wavelength somewhere north of the calibration and continuously tune it down, making it shorter. Not until we reach the calibration will our receiver have any clue what’s going on, given our receiver is incapable of making sense of waves longer than that. At ~1160 nm, however, we achieve one calibration axis — perfectly aligned with the direction of wave propagation initially — and finally the sensory bells start ringing harmoniously. At this point the picture resolves to that of a one dimensional world.
As we continue to tune down, a transition axis swings into view, initially so nearly parallel the wavefronts that it measures just shy of infinity, hyperbolically speaking. As it does, our first calibration axis will drift askew in order to maintain the calibration. These two phenomena occur at the same rate of angular displacement, right up until the next critical wavelength is reached — ~821 nm — 1/√2 the calibration. At this point our latest axis has fully transitioned to become the second calibration axis, and we are in a two dimensional world.
Further tuning swings another new transition axis into view. Once we tune down to a wavelength of ~670 nm — 1/√3 the calibration — that axis has fully transitioned, and we get a sense of our first pure color — red. At this point the reference frame is positioned such that there are 3 calibration axes and no transition axes.
We continue tuning down, and another new transition axis swings into view. By the time we reach ~580 nm — 1 / 2 the calibration — it becomes another calibration axis, making four total. This is sensed as yellow.
All four of these axes maintain their measurement as we continue, swinging a fifth axis into view, achieving parity with its predecessors once ~519 nm is reached — 1 / √5 the calibration. This is sensed as green.
And so on.
To put it crudely, the closer together the waves get, the more calibration axes are needed, and there will always be either 0 or 1 transition axes — 0 in the case of pure colors, 1 when in between them. All other axes remain orthogonal.
If we assume the perspective of the point at the center and gaze into the incoming waves, it’s as if they bear different shapes in the sky — red triangles, yellow squares, green pentagons, and so on. Or, if we’re ready to take the next leap, perhaps sense of red, for example, is not fundamental but rather tantamount to a sense of “three” — at a particular calibration, of course. This could suggest that, underneath it all, basic number sense is what higher order sense like color reduces to.
At this point we’ve clearly taken a few more leaps — we’ve not only correlated the wavelengths of color spectrum apices to a sequence of inverse square roots, but we’ve related that sequence to an abstract notion of wavelength. Furthermore, we’ve introduced the concept of a variable number of dimensions per interaction, based on wave fields and radiating spheres and whatever.
Let’s keep going — continued over here.