How did we end up so far down the rabbit hole ?
We were talking recently about how did we end up so far down the rabbit hole with wishdrops, weighing whether the whole thing might be a delusion. And though we do use the term wishdrops as a generic pronoun, not to mention in every form of speech, what we mean this time is the alt physics we’re always talking about.
Another thing specific to this time is that we’re only trying to explain how we got here, so we’re going to be even less persuasive than usual if you can believe that. We’re just gonna straight up tell you about the leaps of faith we made to get here — more of a therapy session than a thesis defense.
If you’re wondering where “here” is — like what is the latest in wishdropland ? — it could be the part about the universe having as its latent form an infinitesimal sphere of infinite dimension, a phenomenon we like to call dilation of the omnipresent point, because we said that once and thought it sounded pretty cool, plus it would be apt if the infinitesimal thing were true. These are just fancy ways of saying the actual structure of what is known as the universe is so small (albeit of infinitely many dimensions) that every point in space is arbitrarily close to each other (which bodes well for portals and prayer and other spooky action at a distance), yet somehow we perceive it as the expanded projection we are familiar with (we’re actually wondering whether traditional space merely represents “the long way” to go anywhere).
Let’s write that last sentence again without the parens and italicize it for emphasis:
These are just fancy ways of saying the actual structure of what is known as the universe is so small that every point in space is arbitrarily close to each other, yet somehow we perceive it as the expanded projection we are familiar with.
Probably should have led with that. Anyway, we took it even a couple steps further, but we’ll get into that when we get there — we have a long way to go so we might as well get started.
Does physics model everything ?
It seems like a common thing to assume yeah, physics probably doesn’t leave any particle unturned when it comes to describing the behavior of the universe — the weirdness of quantum mechanics notwithstanding — but thoughts, feelings, and life processes in general ? Trials, passions, and the “energy” we bring to bear on them ? That stuff is more magical — a notable exclusion from physics.
Our contention is well is it though ?
Our first leap is to assume biology, underneath it all, is governed by the same laws that dictate what happens when apples fall, or when heavenly bodies dance, or when particles annihilate — the laws of physics. It’s hard to tell how much of a leap it is, to be honest, since we took it a long time ago and all but forget what it was like before that, plus maybe everybody else is already there ? Let’s keep going just in case… ahem.
Sure, biology would represent much more sophisticated and higher order operations, but our guess is that biological activity ultimately relies upon and delegates to physics — similar to how modern programming languages compile into basic operating system instructions. We mean this not only to apply to small scale, hyper localized biological processes, but rather to cover the gamut — micro, macro, flora, fauna, growth, emotion, reproduction, love, and so on — at all levels of the fractal.
One way to think about it is to peer out the second story window across the grassy corridor where the power lines run, flanked by majestic leafy ramparts and home to hundreds of birds, critters, and insects, and mentally overlay the vista (using imaginary special glasses) with the teeming radiation that closes the biological circuitry in order to anticipate plant and animal growth and movement (unless that’s all just coming off the power lines ?). Our guess is that the life force we are all so familiar with is not something aside from physics — it is physics — or built upon it at least (a strong complement at the very least). In our imagination, the trees out there know where and how to grow not just “because DNA” but because the invisible radiation network composed of all living things suggests which part of DNA to pay attention to in any given locale.
We’re guessing human bodies work this way too, and that the abstraction is yet greater, furthermore accounting for collections of thought and thought collectives — the history of everything and the telepathy to share it — all in a common format. If we want to learn more about Atlantis, for example, all we have to do is meditate — that’s pretty much what we’re saying (not really but still).
Is there anything physics doesn’t cover ?
There is one “hole” we cannot convince ourselves doesn’t exist — what we have come to call the “spirit window.” Essentially that which mediates consciousness. The problem we face is to wonder how thought is eternally capable of analyzing all prior thought, a trick a computer, no matter how capable, can never accomplish. A computer would need an instruction to analyze its last instruction — but then where does that instruction come from ? And how is it subject to analysis once it executes ? The agent must exist outside the system at every iteration before becoming a part of the system. We face a conundrum similar to those expressed in Russell’s paradox and Gödel's incompleteness theorems, as this fine post articulates — we simply cannot conceive of formalizations that account for everything.
If the laws of physics, including consciousness, form a complete dictionary, describing all words, but only in terms of other words, how do we bootstrap ourselves into understanding the first word ?
Our leap here is to assume physics models everything — except the spirit. And that the spirit has a special power to invoke the universe and divine its meaning. While “universe” technically implies a “closed system” — meaning subject to no external influence, and therefore self-consistent — we mean it only colloquially to refer to that which obeys physical laws. This notably intimates that our universe is rather an “open system,” per terminology and belief structure, subject to the influence of external spirits in particular.
Now we have no problem pushing the spiritual boundary back as far as possible, well beyond conventional physics, allowing for biological signaling to cohere as much as necessary on the inside of the universe before delivery across the boundary — and in reverse in response to spiritual exertion, if free will is a thing — always abiding by the rules, we assume, even if we don’t yet understand their breadth. Ultimately, however, we take for granted that a spiritual boundary exists. We tend to imagine it takes the form of the tiniest sphere, if not a point, and are comfortable assigning little spirit holes to every “node” in the physical system, including what are thought to be instances of fundamental particles — the consciousness of electrons and photons and so forth. Not sure if that part comes as a surprise or not.
We do have a further thought on externalized spirits — one that may invalidate the entirety of the position we just articulated — but it is based on everything else we’re about to describe, so please bear with us and we’ll come back to it at the very end.
Now if we accept this leap, even temporarily, just as a thought exercise, what would this mean for the spirit independent of the physical system ? Given the physical system is responsible for modeling everything except agency, presumably the spirit apart from the universe would know nothing about planets, stars, colors, music, friendship, camaraderie, memory, body parts, language, or even time and space itself. Or maybe it would, but with no ability to sense any less than all things at once ? Speculating, obviously, and furthermore about nothing provable, but gees — seems pretty bleak (thank goodness we have a universe to play with). Or blissfully glorious, who knows, plus whatever, the idea gives us a foundation from which to take our next in a series of great leaps all the way to the bottom, so let’s keep going.
Are all senses spectral ?
If physics is to account for, well, almost everything, but among almost everything, the five or maybe more senses, then where do we even start to guess how ?
Well, what do we know about the connection between physics and sensation ? As it turns out there is a Rosetta Stone, or maybe even two, or maybe it’s just one because didn’t the original actually relate three different scripts not just two ? Or whatever, these two truths could give us a kickstart:
what we perceive as color maps to electromagnetic wavelengths and frequencies (light waves, basically)
what we perceive as musical notes maps to compressed air wavelengths and frequencies
Furthermore, both spectra can be construed as having seven consonants, even though Newton proposed seven colors expressly because there were seven primary notes in a scale, so maybe we’re cheating ? Anyway, the colors he proposed were:
red
orange (new at the time)
yellow
green
blue
indigo (new at the time)
violet
And the notes, perhaps obviously, would be:
C
D
E
F
G
A
B
So we take this leap, and of course we’re all in now, believing all senses follow a similar pattern, even as we are yet unaware of how the other spectra manifest in the real world. Now if we haven’t found, or perhaps cannot find, the waves we’re looking for, what else can we do ? Is there any other evidence of their existence ? In particular, is there anything about the spectral profile that matches what we know about the other senses that might in turn hint at the existence of undiscovered or invisible waves ?
This is where our next sense comes in. If we add a third, though perhaps uncommon, “sense” — the sense of direction — we can refine our philosophy to suggest all sensory spectra comprise three plausible opposites and one other consonant to represent their balance. In the case of sense of direction it’s sort of obvious:
backward — forward
left — right
up — down
center
But for colors and notes it’s not much of a stretch either, given complementary colors and perfect fifths are real things. As for which colors and which notes represent opposing pairs, we’ll leap straight into matching 1 with 4, 2 with 5, and 3 with 6, allowing 7 to be the balance, which doesn’t seem unreasonable in either case, at least we never thought so (plus, spoiler, we’re gonna change our mind later anyway, at least about the colors, so it prob doesn’t matter too much right now):
red — green
orange — blue
yellow — indigo
violet
and:
C — F
D — G
E — A
B
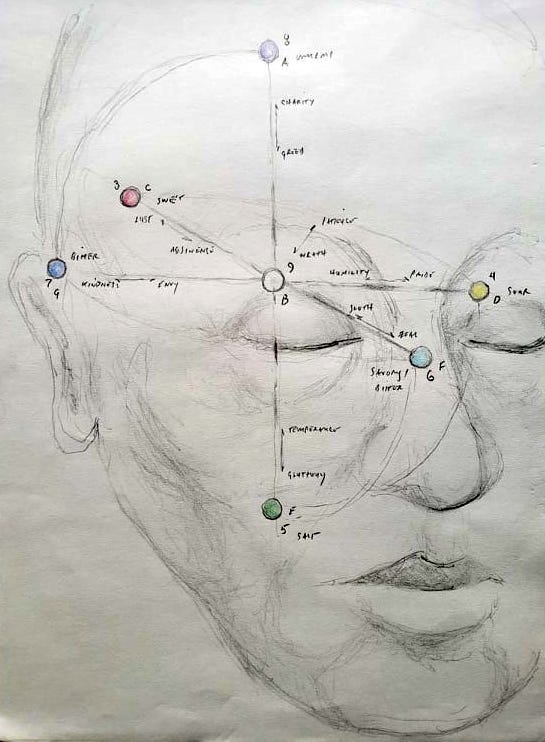
Next we’ll jump to emotional sense, or mood, which obviously needs to be modeled, even if, like sense of direction, it is not a standard issue “sense.” It turns out there is a readily available set of consonants we can borrow for this too, and indeed, we have come to swear by their applicability, even as it is harder to convince ourselves they are spectral in nature — we just know we’re this far down the hole already so what the heck, take another leap. The consonants would be what are well known as the seven deadly sins:
lust ← sloth
pride ← envy
gluttony ← greed
wrath
And they can be countered by the seven chief virtues:
abstinence → zeal
humility → kindness
temperance → charity
patience
Let’s try to rationalize these a bit.
The sins, it seems, are what we feel in the absence of exertion. The left sides — lust, pride, and gluttony — are the sins of impulse; they can be fed, without exertion, and represent a pull toward the individual. The right sides — sloth, envy, and greed — are the sins of inaction; they are not fed, but also imply no exertion, representing a lack of give from the individual. This establishes three axes, each directed from the collective toward the self. Furthermore, one axis is dedicated to each of body (lust ← sloth), soul (pride ← envy), and mind (gluttony ← greed); or id, ego, and superego if you’re more psychoanalytic and less new age (in truth we are still wondering whether superego doesn’t correspond to agency or the spirit instead of the mind, but we’re in therapy mode not thesis mode so we’re off the hook and let’s just hand wave at it and keep going). Wrath is taken not strictly to imply some form of anger, but rather impaired ability to let impulses go, increasingly so as the sins of impulse are fed.
We are clearly taking liberties with the definitions of the words we are using — not to mention the relationships between them. Spirit and soul we mean very differently, for example, even though they are commonly used interchangeably. Spirit to us is not much more than consciousness, and soul is more the wellspring of persona, or ego (another word with divergent colloquial meaning, we suspect). And gluttony we put on the mind axis, though it is commonly associated with, like, eating. We rather think of it as taking material “stuff” for the self, the idea of which is responsible for the associated feeling.
The application of these words may be oblique, but the intent is direct — our leap here is to accept that the base emotional complex, abiding by the same spectral profile that all senses do, is the original inspiration for the sins, the virtues, and Freud’s psychic apparatus. In other words, there is some underlying truth about the way we feel things that is the basis for the development of these models. Moreover, that truth is physical — not magical — strictly encoded into the laws of the universe. As for why this point is obscured by its chosen descriptors, we take another leap to assume their meanings have migrated over time, subject to whatever translations, unwittingly abandoning any connection to the spectrum somewhere along the way.
The virtues represent the remedies to the sins — exertion, basically. The same axes would apply, but in opposing directions respectively, meaning from the self to the collective:
abstinence → zeal (body, or id)
humility → kindness (soul, or ego)
temperance → charity (mind, or maybe superego)
The left sides — abstinence, humility, and temperance — represent exertion to resist the internal pull of the impulsive sins. The right sides — zeal, kindness, and charity — represent exertion to overcome the sins of inaction. A common theme across virtuous exertion is that it introduces a latency to, or a lessening of, the effects associated with the instinctual sins. Patience, it would follow, takes advantage of this latency, and correlates to a less impulsive self.
Following the psychoanalytic parallel, it would seem the self needs its body and soul and maybe its mind fed. This happens naturally through sin, but as alluded to in the case of virtue, exertion has a residual effect, leaving some form of energy — a charged cloud, or an abstract “halo” — from which the sink that is the self can draw. In this mechanism the halo would forever diminish, decaying per some half life, or weakening until some expiry date, introducing a need for continuous replenishment. This probably means we should keep up the exercise in all three phases of the game — body, soul, and mind — such that we need not resort to too much sin to satiate, given sin begets sin, in this fake model and perhaps in real life, too.
Ok, enough pseudo religion and self help, and apologies for blurring the lines between feelings and actions if we did that — the point was only to observe that a wide range of senses, in fact all of them we assume at this point, can be modeled in roughly the same way, with corresponding spectra that share the same profile, perhaps even on the same spectrum but at different energy levels ? This makes it plausible that some small set of rules, maybe even some of the same ones we already know from physics — involving force and charge and mass and so on, though we obviously don’t yet understand how — describe the way senses work.
There are a few other senses we’ve thought about but have yet to mention, including taste:
sweet — soft bitter (or savory ?)
sour — hard bitter
salt — umami
savory (?)
Not sure about these at all, but the left sides could pass for a progression of the impulsive — or compulsive ? — tastes, the right sides, their opposites, and savory, who knows ? But at least there are sevenish with some opposite action going on. Also, wanna know something weird ? Sometimes we have the inclination to put garlic as the balance. It’s just this nagging intuition, even less defensible than usual for us, and that’s saying something. Maybe it has something to do with warding off vampires ? Plus the taste.
Also there are chakras, conveniently already mapped to colors, body parts, and emotion, really tying the room together, not to mention a whole bunch of old religious symbols, like the six pointed star, the menorah (three pair of opposing candles balanced on a central one), and the cross, obviously (if you feel compelled to reduce to just two axes, pluck the body axis, for it is merely flesh and blood). Basically everywhere we look we find a way to shoehorn whatever we see into the scheme is what we’re saying.
About sins and virtues and old religions in general — yeah, it might seem really out there to pretend they’re based on spectra we’ve never discovered, but it might also seem like wow, did our ancestors already know this stuff ? The latter is customarily preferred in wishdropland. In fact, there should be a word for the fallacy of assuming we’re so much more enlightened now than we were then:
wishdropia — the state of recognizing that our ancient ancestors were more enlightened than we are; not succumbing to the misguided assumption that the arc of enlightenment is always trending upwards
We’ll keep working on it.
At this point we’ve developed a pretty good matrix of sensory spectra, which is conveniently depicted on just three axes. Now peer deep into that structure and ask yourself — where are the wavelengths ?
Do the apices of the color spectrum represent a sequence of inverse square roots ?
Take a look at these vectors:
1
1, 1
1, 1, 1
1, 1, 1, 1
1, 1, 1, 1, 1
1, 1, 1, 1, 1, 1
1, 1, 1, 1, 1, 1, 1
1, 1, 1, 1, 1, 1, 1, 1
1, 1, 1, 1, 1, 1, 1, 1, 1
They range in dimension from one to nine. The question is how long are they ?
The length of any one of these vectors is the sum of its components, but we’re not talking simple addition here. Since the components are orthogonal — each corresponding to a unique dimension — the distance we are interested in can cut the corners. Imagine the components assembled end to end — each intersection a right turn. How do we figure out the length of the straight line from the origin to the end of the last component ?
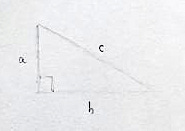
The answer is we use a magical little thing called the Pythagorean theorem. It states that the length of the sides of a triangle with a right angle in it have the following relationship to each other:
a^2 + b^2 = c^2
a and b are the lengths of the sides involved in the right angle, and c is the length of the side opposite the right angle, otherwise known as the hypotenuse.
This formula is pretty popular, we can read about it pretty much anywhere. Not sure how Pythagoras came up with this one, but given how blatantly awesome it is, we are compelled to wonder — in the full spirit of wishdropia — what else did he know ?
Since our components are all orthogonal to each other, right angles between them are implied, and so the thing we’re after — that shortcut distance from the start of one component to the end of another — is indeed something we can calculate using the Pythagorean theorem. The simplest case is the two component vector:
1, 1
The two components would be a and b in our calculation — and we want to know c. If a = 1, and b = 1, then a squared plus b squared = 2, which means c = √2. This is the length of our hypotenuse, and, yes, the length of our vector in the two dimensional case.
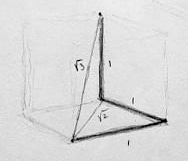
What about in three dimensions ?:
1, 1, 1
Remember, every component is orthogonal, and guess what — that applies to combinations as well. As long as vectors don’t share components — as long as there is no overlap in the dimensions represented — vectors will always be likewise orthogonal. This means more right angles, which in turn means more Pythagorean theorem, please. In this specific case, our two dimensional vector of length √2 forms a right angle with any other component tacked on to its end.
In other words, we can use the Pythagorean theorem again to calculate the length of the three dimensional vector, except this time a = √2 (and b = 1 again), so a squared plus b squared = 3. As such, c = √3.
A pattern is emerging. If every component is length 1, as we’ve drawn it up, then the length of the vector, from the origin to the end of the last component in the assembly, is always the square root of the number of dimensions:
1 — length = 1
1, 1 — √2
1, 1, 1 — √3
1, 1, 1, 1 — 2
1, 1, 1, 1, 1 — √5
1, 1, 1, 1, 1, 1 — √6
1, 1, 1, 1, 1, 1, 1 — √7
1, 1, 1, 1, 1, 1, 1, 1 — √8
1, 1, 1, 1, 1, 1, 1, 1, 1 — 3
How beautiful ! :)
Now consider this corollary exercise — what if we want to fix the length of the vector to 1, but evenly distribute the components in a variable number of dimensions ?
It’s quite simple, actually. To scale each vector to length 1, simply divide 1 by the length we calculated — then go back and apply that same ratio to each component:
1 — length = 1
1/√2, 1/√2 — 1
1/√3, 1/√3, 1/√3 — 1
1/2, 1/2, 1/2, 1/2 — 1
1/√5, 1/√5, 1/√5, 1/√5, 1/√5 — 1
1/√6, 1/√6, 1/√6, 1/√6, 1/√6, 1/√6 — 1
1/√7, 1/√7, 1/√7, 1/√7, 1/√7, 1/√7, 1/√7 — 1
1/√8, 1/√8, 1/√8, 1/√8, 1/√8, 1/√8, 1/√8, 1/√8 — 1
1/3, 1/3, 1/3, 1/3, 1/3, 1/3, 1/3, 1/3, 1/3 — 1
And so for a vector scaled to length 1, the length of each component, if evenly distributed in n dimensions, is given by this formula:
1/√n
Nice — so what’s the significance ?
We submit the above elaboration for your enjoyment, but also because we are hereby taking another leap, perhaps our greatest yet, and certainly our most specific — we’re suggesting this pattern is inherent in the wavelength ratios of the pure colors on the spectrum. Indeed, if we calibrate our numerator to a wavelength of somewhere around 1160 nanometers, the sequence looks like this:
dimensions = 1 — ratio = 1 — λ = ~1160 nm
2 — 1/√2 — ~820 nm
3 — 1/√3 — ~670 nm — red
4 — 1/2 — ~580 nm — yellow
5 — 1/√5 — ~519 nm — green
6 — 1/√6 — ~474 nm — blue
7 — 1/√7 — ~438 nm — indigo
8 — 1/√8 — ~410 nm — light violet
9 — 1/3 — ~387 nm — deep violet
The internet suggests that’s not bad for the color to wavelength mappings, though you may notice we’ve skipped orange. Oh, and that we have two violets (the second of which only briefly registers before fading out). Are we saying orange is just a mix of red and yellow — not a true apex ? Perhaps only a “minor note” ?
Who knows ? What we do know is we sort of have to live with the orange exemption for now, even as we keep our mind open to possible explanations, because, for better or for worse, our belief has taken root; which, again, doesn’t mean it’s true, but it does explain what is just one stepping stone beneath our feet in a long series of leaps. This one in particular we might call the “gates of wishdropland” — a narrow passage to the vast, mysterious, many-dimensional world we’ve been trawling ever since.
***
If you made it this far maybe jump over to part 2 and see what happens :)