Seems like there is a lot of math in the universe. Equations of mass and energy, fractal patterns in nature, engineering projects like your back deck, and so on. I mean seriously, what doesn’t math cover ?
If you didn’t assume that last question rhetorical, your mind may already be wandering. Otherwise, well, this is really what we’re talking about, so let’s do it — what kinds of things have aspects that cannot be precisely modeled ?
Human life processes ? Sure, there’s plenty of math to measure and apply, in medicine, genetics, economics, sabermetrics, whatever, but is there fuzziness around the edges, would you say ? Same question about biology in general — you know, nature — migration patterns, algal blooms, circadian rhythms, math, yes, sure, but is anything else going on there ? Or what about art ? Obviously there’s a Golden Ratio, and perhaps other principles of beauty, but is all beauty accounted for ? And thought itself ? Psychology is a science, people are predictable, formulaic movies make us cry, is it all a calculation ?
Here’s one — the basic building blocks of the universe. You may wonder about these — even if you aren’t a theoretical physicist — because presumably there is some kind of baseline, or starting point, that is the “given” in this amazing experience. Which is to say that even if you are willing to “go there,” and accept that everything in the universe is a math problem, an equation, a wave function, whatever, then what are the axioms ? What are the pure fundamentals ? What is the starting point when it comes to modeling the universe ?
Current models
Before we get way into it, let’s acknowledge the leading edge of scientific convention on the matter, meaning that which has gained widespread acceptance in the physics community and beyond, starting with the small stuff. There is a well-known model for the particles and forces that have been witnessed experimentally, and repeatedly so, at very small scales. It is called The Standard Model, and it works so well that the model was completed well before the experiments. In other words, it was intuitive enough that scientists knew where to look to affirm the model, and did so, registering advances over the course of most of the last century until it was fully “proven.” It describes seventeen particles — which can be classified based on properties like “spin” and “charge” — and also accounts for three apparently fundamental forces.
Now the big stuff. There is one known force that is not accounted for in The Standard Model, but, were it ever arranged, would probably receive top billing at a fundamental forces charity concert. Yep, it’s gravity. It certainly follows a model, albeit a different one, a model that has proven extremely useful for centuries, particularly addressing the behavior of heavenly bodies like planets and stars and galaxies and stuff, plus less heavenly ones like satellites and rocket ships too, I guess.
In spite of the vast enchantment rendered in pursuit of this doctrine, you may look at this and say, “two models… four forces… seventeen particles… is this thing done ?” And most scientists would probably agree with you, while furthermore considering the uncertainty motivation for further pursuit. For example, the prospect of a new model of the universe that incorporates the two prevailing ones — a Unified Theory, as it were — represents one of the great opportunities in modern physics. And let’s cut right to it — that’s our motivation too ! However, rather than thinking about it in terms of:
What experiments or insights can we conceive of to ratchet progress ?
Since I don’t have any apparatus in my basement, nor a deep understanding of the field, plus I’m just a bit lazier, let’s take another angle:
How would we go about creating a universe if we had to ?
Modeling a universe
We can use the same guiding principle those who take the first approach presumably do when analyzing an imagination gradient — divine the elegance and simplicity. Who knows, by starting at the other end — the more imaginary, less observable one — perhaps we can prescribe a meeting in the middle somewhere, and as it plays out suggest where to seek scientific breakthrough throughout the next century ! But before we even get into particles and forces and whatever, and after we come down from that brief outburst of enthusiastic optimism, let’s start with what may be the true beginning, the only window into the known universe we have — perception.
At some level, despite whatever understanding of the universe we’ve accumulated, it’s always been filtered through perception. But I’m talking more directly than that — how would you model perception ? A receiver of some kind, around which we can build a universe ? To start, you probably wouldn’t choose a weird shape, like a neuron, or anything human, really, or a transistor or a cloud or whatever you can come up with. We’re talking way more generic than that, and, well, bluntly, much more of a starting point. In fact, that’s it precisely — we’re talking about a point. Literally. A zero-dimensional notion of existence. Perhaps an “energy reservoir,” but nothing more. Of course, that probably makes for a pretty boring experience, so, well, since it is up to us, what can we add ?
Actually, before we go any further, let’s go ahead and disambiguate and call our point a “particle.” Same idea, it still takes up no space, zero dimensions and all, it’s just easier to talk about, and let’s be right up front and admit it’s the only kind in our universe, since what could be simpler than that ? In other words, all particles are of this same construction. Which gets to, oh yeah, are we not the only particle ? Because otherwise it would be so lonely ! And, if there is another one out there, there are likely an infinite number, because again, the elegance principle, which we should already be assuming. Particles are presumably strewn across an otherwise vacuous canvas we don’t even know how to describe yet, never mind have any way of knowing about what’s on it. If they are, how do we find them ? Are they yearning to find us too ?
So maybe yearning is another fundamental. Maybe we call it “existence anxiety” — a sense of obligation to dispense with energy in the hopes that some of it will reflect back off something as a beacon of solidarity. All of which is to suggest a vast array of particles dispersed on a canvas, all of them crying to be heard. Well, in order to hear and be heard, we probably need a shared medium of some kind. Something into which we can release a “pulse” of energy such that it carries away from us and toward prospective recipients. We won’t even call it space yet, because that requires dimension, which we have not yet introduced. Furthermore, how can we distinguish release from restraint, or one pulse from another, without the notion of elapsing ?
Alright, let’s not belabor this, we need space and time (I do sort of suspect one could devise a beautiful derivation of the origins of space and time, I’m just sort of stuck on how to do so in context at the moment). Space to make sense of our canvas — which, for whatever it’s worth, we’ll continue to consider an underpinning that is independent of the space we stencil onto it — and time so that our picture becomes a movie. Let’s also admit that our canvas is capable of carrying waves, or pulses of energy released from particles, even if we don’t understand those waves yet. Maybe those waves are a native feature of the canvas, maybe they are supported by the wayward forces of somewhat uniformly distributed particles “thatched” together to form a sort of fabric draped over the canvas — either way, the canvas is capable of wave propagation.
About the space that lends shape to our canvas, well, how many dimensions are we talking about here ? Three would seem the obvious choice, since it seems to work pretty well for our world, no ? Unless you are a fan of the Holographic Principle, in which case you might prefer two ? Or an M-theory proponent, in which case you may like nine or maybe ten spatial dimensions ? Or a Cubist painter, in which case who knows how many dimensions are your preference !
You know what though ? And this is what I really wanted to talk about from the very beginning — I don’t know why one choice would be better than another. Where is the elegance in choosing a specific number of dimensions ? And so here’s a theory, or more of a conjecture, I suppose —
There are an infinite number of number of dimensions in the universe.
Not just an infinite number of dimensions, mind you, but rather an infinite number of “reference frames” — grids, spaces, whatever — around each particle, each frame of a different number of dimensions. I guess that makes it like infinity squared dimensions per particle, or even infinity factorial, which probably calculates to infinity again, but that’s beside the point, plus I probably got that wrong anyway. The point is that the reference frames are all superimposed on each other. There’s a one-dimensional frame, a two-dimensional frame, a three-dimensional frame, and so on, for every single particle, including our focal point of perception, and moreover, every frame sustains real interaction. They each reveal the rest of the particles and waves on the canvas, thereby contributing different views of the same information, resulting in different effects, their sum a cohesive reality.
Perhaps the frames around a particle accumulate in orientations of “optimal utility,” so that a maximum is drawn from the canvas with each additional frame. Perhaps optimal utility involves contrasting rotations among the frames, in order to elucidate wave patterns. Visualize a one-dimensional rod, a two dimensional plane, and a three-dimensional space all pivoting around a single point and slicing through each other in fluid movements to highlight waves in the vicinity. Almost like lasers of different colors and shapes sweeping through patchy fog. Now add a few more higher order spaces, and, hey, why not, keep going. Heap on a thousand reference frames while you’re at it, each of a different number of dimensions, at least one of a thousand dimensions, provably.
At what point does this apparatus capably support abstract thought ? Consider, for example, what it means to “zoom out” of your own thoughts; to “bump it up a level” in conversation; to “summarize.” How are we able to do that ? How are we able to so deftly rotate through a variety viewpoints in everyday decision-making, almost involuntarily ? From what derives the ability to think in metaphors and analogies, where similarities between disparate relationships are gifted to us from the subconscious in everyday conversation ? What is the basis of Number Sense ? Is it all in an attempt to analyze one set of information by framing it numerous ways — literally ?
Or, going back to the very beginning, maybe these sorts of things can’t be, and therefore aren’t, modeled precisely.
But if they can be, I wonder if this is the basis for a plausible model. An infinite number of reference frames, each of a different number of dimensions, all to process one set of information. A model in which energy originates at an otherwise zero-dimensional particle, emanates in waves over a canvas until, on the receiving end (another particle), those waves are refracted through superimposed reference frames, or grids of orthogonal dimensions, such that they manifest in different perspectives, to overlapping effect (not unlike a Cubist painting, come to think of it). And so perception is not confined to one particular grid or another — it is the layered grids of varied dimensions applied to the canvas that constitute an attempt to make sense of the waves thereupon, involuntary or otherwise. To jump ahead a bunch of chapters, imagine your head as a sort of “wave chamber,” in which the superposition of innumerable juxtaposed electromagnetic wavefronts washes over a single point of perception, the focal point of an infinite number of reference frames, each of a different number of dimensions, oriented such that the overlapping projections form useful images. That’s where we’re trying to go with this.
OK, slow down
That’s a lot to process. Let’s go a little slower, and not jump straight into a specious connection to complex thinking.
Start with one dimension. Assume our lone dimension stretches forward and backward from our perception particle. Well that’s something ! Maybe that gives us a sense of “inside” and “outside” — within yourself and without — obviously pretty abstract, but definitely not nothing. Also, if our one-dimensional space is a projection of our canvas, what do waves look like ? We haven’t really talked about how far we can “see” into a reference frame — whether we can see the whole thing or only from the vantage of our particle — but most likely all we’d get from the one-dimensional grid is the timing of waves as they arrive at either the front door or the back door.
Add a two-dimensional space. Now you have a panoramic view. You would have a sense of direction, except where is the “mark” that enables you to distinguish “left” from “right,” say ? Or “me” from “you” ? Maybe that’s why you need the one-dimensional frame superimposed — it provides orientation for the second frame.
Then you add a third frame, one of three dimensions. If the frames are of fixed orientation, the extra dimension on the third is presumably orthogonal to the plane cut by the second, but more interestingly, perhaps the two dimensions of overlap are “out of phase” by half a right angle, such that the second and third frames provide different information, because, well, the more the better. And of course, like the first to the second, the second provides an orientation for the third, which could give us sense of left, right, up, down.
Now let’s add a four-dimensional frame. Four dimensions is two superimposed two-dimensional spaces, and we already have one of those. In fact, if you squint at the picture and consider the first two of four dimensions in aggregate, and, separately, the second two as well, you’ve once again reduced to a two dimensional space. This may mean that perception of four dimensions is rather obscured by that of two. Maybe this is a clue as to why the space we live in isn’t obviously four-dimensional. And a clue as to why hey, I just realized prime numbers are interesting again ! I always thought they were cute, sorta quirky, but otherwise, eh. All of a sudden, though, they seem like one of the most important concepts in the universe, if you accept our purely mathematical premise, since only a prime number of dimensions fails to reduce.
By the time you get to five, I’m just not sure how to assess the value, despite its primeness, but I haven’t thought about it very long. Same with six, which is the cross of two and three, and so there is a lot of resonance here, superimposition, whatever, but again, not much to add, haven’t thought about it, really.
On the seventh dimension the lord rested if you know what I mean.
Eight and nine get interesting again, and in fact, here is the only really good observation I can fabricate from the real world that might corroborate this whole conjecture. I suspect it is due to a sort of hyper-resonance that occurs because eight is two exponent three and nine is three squared. Take a look at this picture I like to call “the stations of the cross,” even though I’m totally borrowing that title from somewhere else, sorry, it’s just too appropriate to deny:
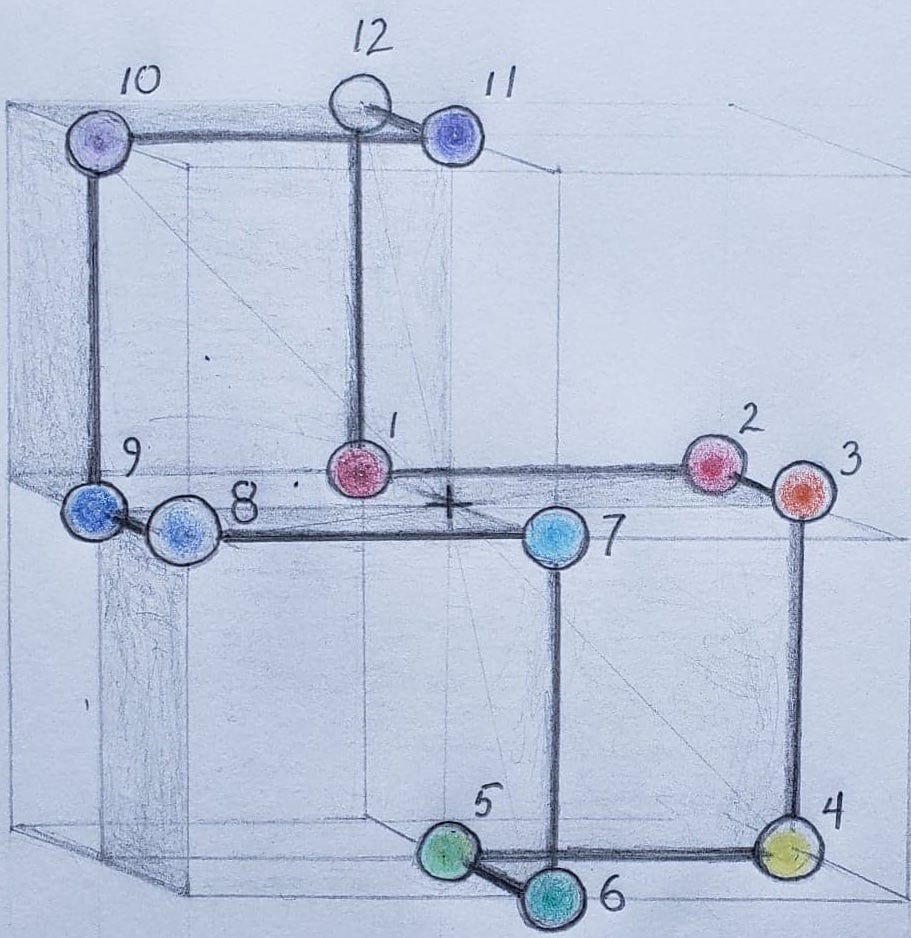
There are twelve “stations” around — or vectors out of — our focal point of perception in the middle. It is meant to depict anything we perceive as a spectrum, such as colors, musical notes, and I would suggest taste, mood, and even sense of direction. The basic idea would be that half of the twelve vectors are consonant in eight dimensions (the even ones) and the other half in nine (the odd ones).
If you look closely at the color spectrum, you’ll notice some interesting things. First, the visible light spectrum appears bound by frequencies that are roughly different by a factor of two, or are, in other words, in the traditional sense, “harmonic.” This could suggest the visible light spectrum occupies one “energy level,” or one trip around the structure in our illustration. You’ll also notice, in pictures such as the one on this page, that the different colors on the spectrum have different profiles — some are sharp, some are blurry, for example. In particular, it seems like there are four sharp spots, evenly distributed and corresponding to our every third vector: 1 (red), 4 (yellow), 7 (cyan), and 10 (purple). This could be due to compounded resonance, since indeed, the proposed model represents lower dimensional spaces as well. And for whatever it’s worth, some forty energy levels away (by a rough calculation), notes of music would correspond to these colors, accounting for several trips around this very same spectral sense spiral, one for each octave. Notes, of course, are famously represented by twelve consonants on a scale.
So what is the connection to eight and nine dimensions ?
Well, the picture is intended to depict all reference frames superimposed, including those of eight and nine dimensions, even though you have to do a bit of mind bending to see it. It looks like a three dimensional cube, but let’s talk through how you might see additional ones.
To see nine dimensions, imagine it is actually three superimposed three-dimensional cubes, each with one dominant axis — backward-forward, left-right, or up-down. Or, similarly, associate each three space with the shaded sub-cube whose lowest number is on one of those axes — 1 (backward), 5 (down), or 9 (right). The dimensions extend out infinitely, so they are not confined to cubes, we’re just cheating by using them to see overlapping things at once.

To see eight dimensions, consider the three axes that cut diagonally across cube faces — 2 to 8, 4 to 10, and 6 to 12. These axes obviously exist on the same planes those faces do, all cutting through and intersecting at the center point. From the center point, any set of three points taking one from each plane constitutes an eight-dimensional vector.
Now take the first sub-cube. Imagine each of the three faces showing on the cube actually represent three dimensions in aggregate, making our cube nine-dimensional.
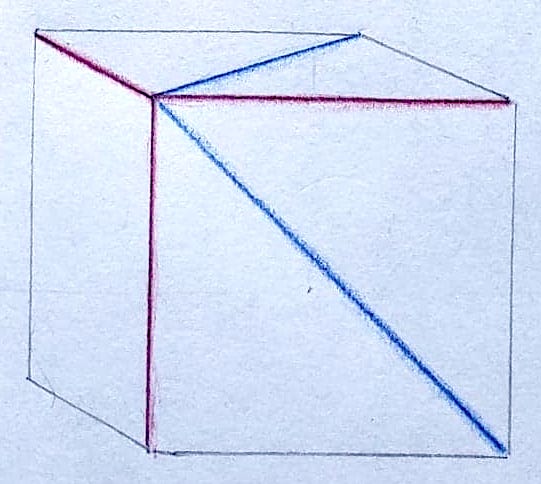
And consider the two diagonal lines on it. Imagine they each actually represent four dimensions in aggregate, making our cube eight dimensional. The cube is now a representation of both eight and nine dimensions.
Now let’s use these spaces. Imagine concentric spheres around the common point at the corner — one of eight dimensions, one of nine (I know, it’s hard to imagine spheres in more than three dimensions, so just picture the regular kind and pretend). Set radii based on a common coefficient, for example:
1, 1, 1, 1, 1, 1, 1, 1 in eight dimensions
1, 1, 1, 1, 1, 1, 1, 1, 1 in nine dimensions
Whether you work with the cube or all these 1s, you can use the Pythagorean theorem to determine the ratio of the respective radii is √(8/9). Guess what else, though ? That same ratio — or very close to it — is the ratio of observed wavelengths for adjacent colors — vectors 1 and 2 in the diagram, for example (or between adjacent notes in a 12-scale, where the observation has more clarity).
Well isn’t that an awesome coincidence !
Of course, the thought would be that they are exactly the same ratio — maybe even definitionally — but why ?
Radius we can consider a proxy for wavelength, because presumably we are concerned with waves arriving at the center point from any direction — thus a sphere (defer any thoughts on the precise mechanics for now). But why would waves of a particular length have a particular orientation ?
The idea is that maybe they don’t. Maybe perception naturally divines the simplest applicable frame — and the simpler the frame, the more pleasing the sense. Maybe the reason it appears spectral is due to the tension in sensing across multiple frames. Maybe your mind is always trying to crush nine dimensions down to eight, for example, manifesting an inward spiral. And maybe it’s time to come right out and make this next level statement, howsoever obvious — maybe the ability to see in more than three dimensions has been hiding in plain sight the whole time !
Let’s not get way ahead of ourselves. Does this ratio really work ? Well, no — not if you need for different “octaves” to relate by a factor of two. Twelve sweeps of half a right angle is (8/9) ^ 6, which calculates to 0.493, so I guess you have to decide for yourself if you think that’s close enough (was there a reason we believed traditional harmonics applied to sense, again ?). Actually, I know I said I don’t have a lot of apparatus, but this seems like an easy one when it comes to devising an experiment. Anyway, here is the proposed color spectrum mapping, based on the best fit I could make from internet images and the ratio:
deep red (*) — 703nm
red — 663nm
orange — 625nm
yellow (*) — 589nm
green — 555nm
green-cyan — 524nm
cyan (*) — 494nm
blue — 466nm
deep blue — 439nm
purple (*) — 414nm
deep purple — 390nm
invisible — 368nm
Also — and I know this is probably egregious disregard for what are probably a million other factors — but if projected, this would map to the note of C in position 1 if middle A were at 409hz, which is low, though not historically unprecedented.
The rest of the universe
Oh yeah, we were going to model the universe. We barely got past perception, huh ? Eh, it took so long though. Hm, let’s forget it for now, except to suggest that it doesn’t particularly matter whether a particle is governed by, or somehow attached to, a manifest human consciousness. Think about all the other things out there for particles to mediate ! Animals, cells (ooh — I wonder if organs have their own “identity” ?), plants (or what about, like, just one branch — I think about that sometimes when I’m admiring a big tree), rocks, the crystal ones and the other kind, probably a bunch of other really cool things I have no idea exist, and, well, maybe some are just dumb atom cores. Picture them all like butterflies floating around each other on sophisticated multi-grid wing complexes, seemingly erratic but faithfully mathematic. The same set of rules could potentially apply for all of them and give rise to everything else, though admittedly it’s a long journey to the Standard Model.
If you want to lean into it a bit, though, imagine “force” is a real thing particles have. Maybe it’s the baseline yearning we talked about, or maybe it’s a side-effect of the simplification engine. Even if it’s only attractive, since we’re creating frames of every dimension, coordinated forces could easily outflank, pull from around the corner, even sneak attack from the back and disguise themselves as repulsion. Attraction refracted through unlimited and overlaid dimension could probably do some pretty crazy stuff, undoubtedly all while making it appear beautifully simple.