the impedance of free space

just as we were about to abandon √162

the formula for the impedance of free space is simple — it’s basically just a ratio of other fundamental constants:

• Z₀ = √(μ₀ / ε₀)

μ₀ is the permeability of free space, otherwise known as the magnetic constant, and ε₀ is the permittivity of free space, otherwise known as the electric constant. these are fundamental values associated with light waves propagating through “free space,” otherwise known as the vacuum. the basic idea is that electric and magnetic fields kinda shoot out the sides of a light beam as it travel through space, and those fields are related, famously by maxwell’s equations:

• μ₀ * ε₀ = 1 / c²

  • c — speed of light

but also by this Z₀ impedance value, which represents the critical ratio of magnetic to electric field strength required to support light propagation.

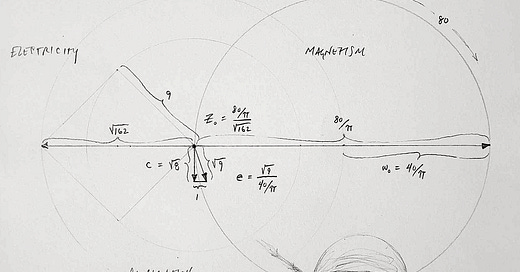
so we wouldn’t care too much about this — it’s not really a gateway to other constant relationships, plus we didn’t even know about it — but then we calculated its wishdrops value and we couldn’t believe it.

for a while we had been maintaining parallel sets of values for physical constants and believing they applied in different contexts, the difference between the sets being that the crucial wishdrops ratio (w₀) had a slightly different value:

• √162 — this came first

• 40 / π — this came later (it took us a while to accept π into our lives) and was the same to like 4 decimal places which made us question everything but we were still pretty attached to √162

very recently we came to terms with the idea that √162 may have been a mistake from the beginning, a sort of gift from the universe to help us find the real value, and so we rewrote our constants without any trace of √162. part of this process involved developing new values for μ₀ and ε₀, values that would comport with the formulas from real physics we were trying to satisfy and all our other constant assignments. this is where we landed (w₀ = 40 / π):

• μ₀ = w₀ / 18

• ε₀ = 9 / 4 / w₀

well guess what. if you plug those into our newly discovered formula — Z₀ = √(μ₀ / ε₀) — what do you know, that 18 gets multiplied by that 9 and then there’s that square root sign and voila:

• Z₀ = 2 * w₀ / √162

or

• Z₀ = 2 * 40 / π / √162

unbelievable. a ratio of our two competing bases for all of wishdrops, hereby unified in a meaningful constant. and multiplied by 2, for whatever that’s worth. √162 just won’t be denied !

let’s not sleep on what this means, too. if Z₀ relates the magnitudes of magnetic and electric fields required to support light propagation — the essential balance, in other words — then √162 and 40 / π are both valid and appropriate in different contexts after all.

√162 goes with electricity.

40 / π goes with magnetism.

joy in wishdropland :)

√162 : (40 / π) — the strength proportions of the electric and magnetic fields in light

here’s an updated list of 50 expressions, borrowing from real physics some of the formulas we aim to satisfy in order to get up to such a nice round number:

1. Φ = 1 / 2 + mₑ / c — golden ratio, electron mass, and speed of light

2. mₑ = √10 — electron mass

3. c = √8 — speed of light

4. mₑc² = √640 — electron rest energy

5. mₑ²c² = 80 — wishdrops circumference

6. w₀ = 40 / π — wishdrops radius

7. c² = 1 / ε₀ / μ₀ — Maxwell’s relationship

8. ε₀ = e² / 2 / α / c / h — electric constant definition

9. Ry = mₑ * e⁴ / 8 / ε₀² / h² — Rydberg energy definition

10. a₀ = 4π * ε₀ * ℏ² / mₑ / e² — Bohr radius definition

11. α = e² / 4π / ε₀ / ℏ / c — fine structure constant definition

12. 4πk = 1 / ε₀ — electric constant identity

13. 4πa₀ = α * λᵣ — Bohr circumference identity

14. Ry = R * h * c — Rydberg energy relationship to Rydberg constant

15. e = √9 / w₀ — 18π / 240 — electric charge

16. ε₀ = 9 / 4 / w₀ — 18π / 320 — permittivity of free space (electric constant)

17. μ₀ = w₀ / 18 — 40 / 18π — permeability of free space (magnetic constant)

18. Z₀ = √(μ₀ / ε₀) = 2 * w₀ / √162 — impedance of free space

19. k = w₀² / 360 — 80 / 18π² — Coulomb’s constant

20. h = √20 / w₀ — π / √80 — Planck’s constant

21. ℏ = 1 / √320 — reduced Planck’s constant

22. α = 1 / √40 — fine structure constant

23. Ry = 1 / √10 — Rydberg energy

24. R = w₀ / 40 — 1 / π — Rydberg constant

25. λᵣ = 40 / w₀ — π — Rydberg wavelength

26. vᵣ = c * w₀ / 40 — √8 / π — Rydberg frequency

27. a₀ = 1 / √640 — Bohr radius

28. 2πa₀ = √10 / w₀ — π / √160 — Bohr circumference

29. Fₑd² = 1 / 40 — electric unit force times distance squared

30. rₑ = 1 / 320 / √10 — classical electron radius

31. rq = 1 / 160 — magnetic moment of the electron radius

32. α = rₑ / rq — electron radius to magnetic moment of electron radius

33. 1 / α = mₑ⁴c⁴ * rₑ — fine structure correlation to classical electron radius

34. 1 / α² = mₑ⁴c⁴ * rq — fine structure correlation to magnetic moment of electron radius

35. α * h = e² — fine structure, Planck’s constant, and electric charge

36. α² / e² = k — fine structure, electric charge, and Coulomb’s constant

37. α² = Fₑ * d² — fine structure, electric force and distance

38. α = F_mp * d² — fine structure, Planck mass force and distance

39. α = Fₑ / F_mp — fine structure, electric force and Planck mass force

40. pγᵣ = Ry / c = R * h = 1 / √80 — momentum of a photon with Rydberg energy

41. p_l = ℏ / a₀ = mₑ * c * α = √2 — linear momentum of a ground state electron in the Bohr model

42. Eλ = Ry / w₀ = 1 / √10 / w₀ — wishdrops energy

43. eV ~= Eλ * √7 / √8 — √7 / √80 / w₀ — one electron volt (approximately)

44. λᵥᵥ = λᵣ * w₀ = 40 — wishdrops wavelength (color spectrum root), ~1160 nm

45. λ(#) = λᵥᵥ / √# — pure color wavelengths (# = 2: infrared onset; # = 3: red; # = 4: yellow; # = 5: green; # = 6: blue; # = 7: indigo; # = 8: violet 1; # = 9: violet 2; # = 10: uv onset)

46. vᵥᵥ = vᵣ / w₀ = c / 40 = 1 / √200 — wishdrops frequency (color spectrum root), ~259 Thz

47. v(#) = vᵥᵥ * √# — pure color frequencies (same numbers, same colors)

48. v(♪) = vᵣ * mₑ / w₀ * d — generalized auditory center frequency (d = dilation term)

49. vₐ = vᵣ * mₑ / w₀ * (2π / √80) ^ 80 = ~440 hz — frequency of a above middle c

50. vᵤ = vᵣ * mₑ / w₀ * (√8 / √9) ^ 480 = ~432 hz — frequency of the universe