spheres and spins and not strings and vibrations

just one sphere, actually

“spheres and spins” and not “strings and vibrations” — that’s the proposal.

just one sphere, actually — of unlimited dimension.

the manifest universe is an unfolding shadow / physics is owed to a fractal geometry / all black holes share a common center / so do all particles / the curvature of space is always perpendicular to the common center / all points in space are arbitrarily close to each other.

these would be some of the implications. let’s try to draw it.

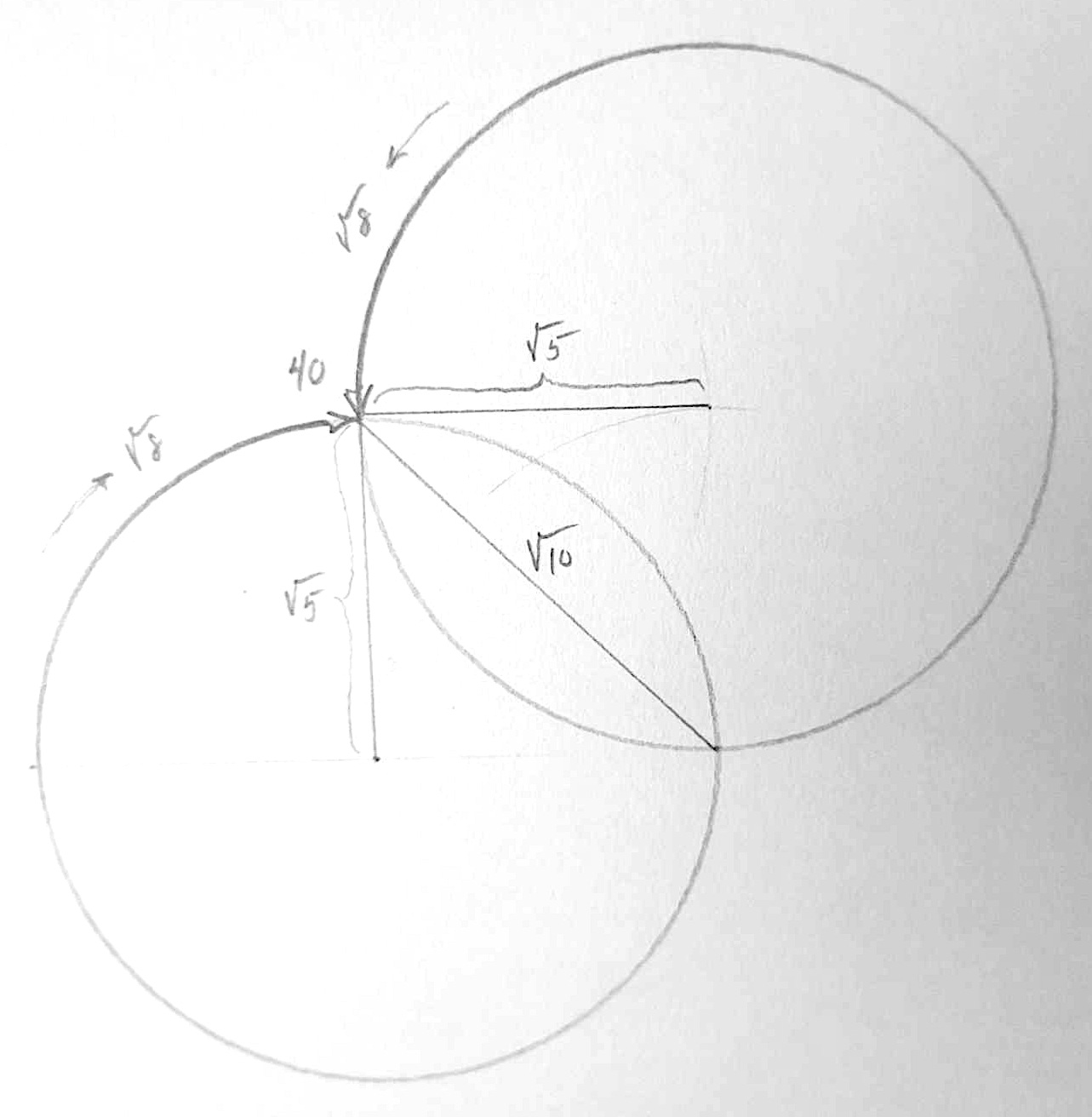
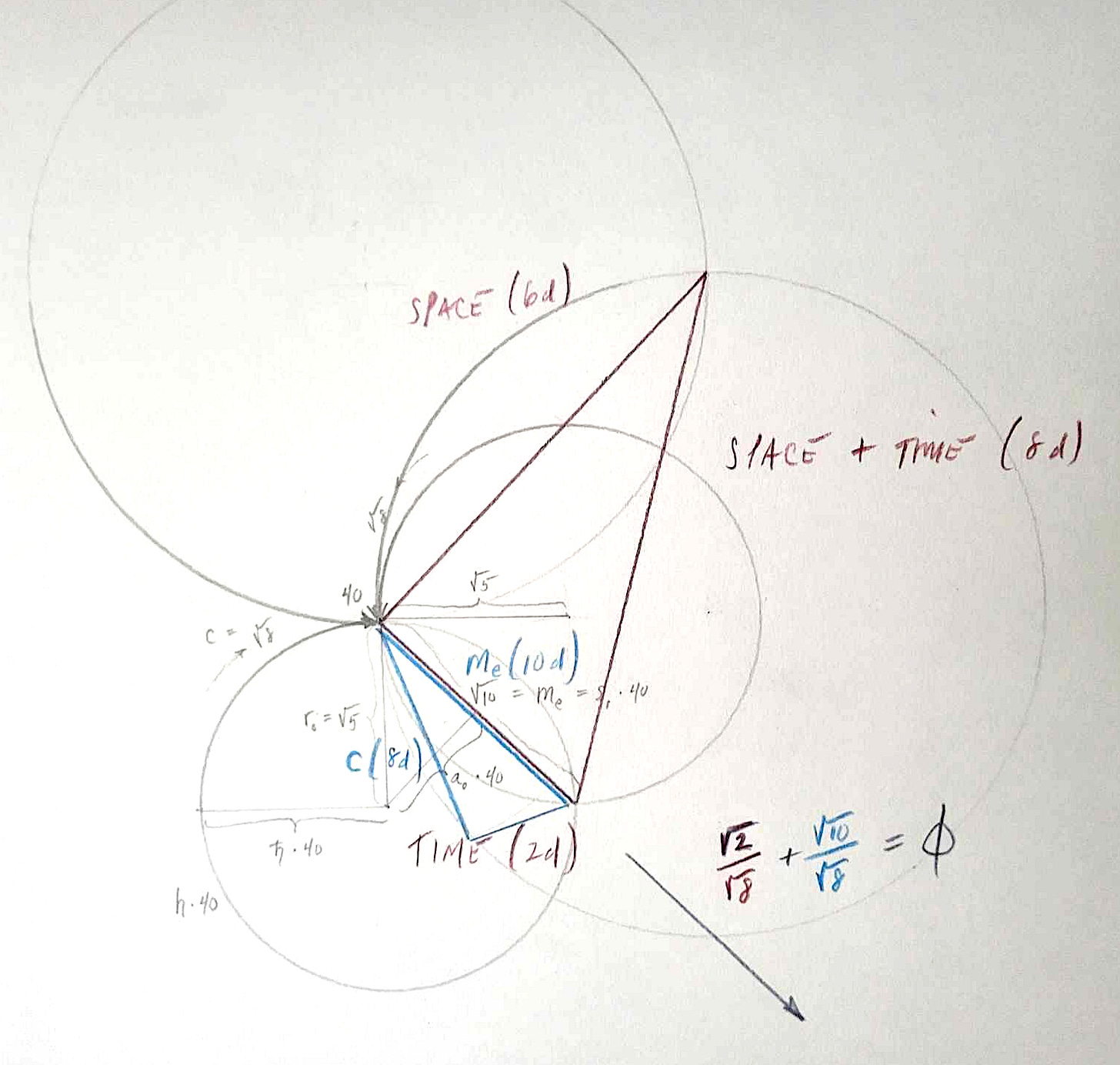
here is a projection of two great circles — circumferences — from the same sphere in a four (or more) dimensional space, spinning at the same rate into a node:

it is projected to help visualize, but in truth:

• the two centers are the same point

• the combined trace is a full diamond (only one side is shown)

• the arrows should both point into (or out of) the page, however secretly perpendicular, combining to represent a new spinning circumference around the diameter shown as √10

the sphere is intended to represent a black hole. its radius represents the innermost stable circular orbit, or the closest possible orbiting radius for matter, which is a real thing in physics. relativity dictates that a precise speed is required to maintain this orbit, regardless of mass:

• c / √6

we’ll come back to this.

the math of the underpinning sphere relies heavily on the pythagorean theorem.

that’s because it is replete with constructs of equal magnitude and perpendicular orientation — radii, circumferences, spin rates — which assemble like unit vectors do:

• √p is the magnitude of p dimensions of “path” or “push” (unit vectors combining end on end)

• 1 / √f is the magnitude of f dimensions of “frame” or “flower” (unit vectors spreading from a common origin into a flat front)

so the integers appearing under the radicals are tantamount to counts of dimensions — combining when in numerators, spreading when in denominators.

within this scheme we assign dimensional ratios to physical constants, though only two fundamentals are needed:

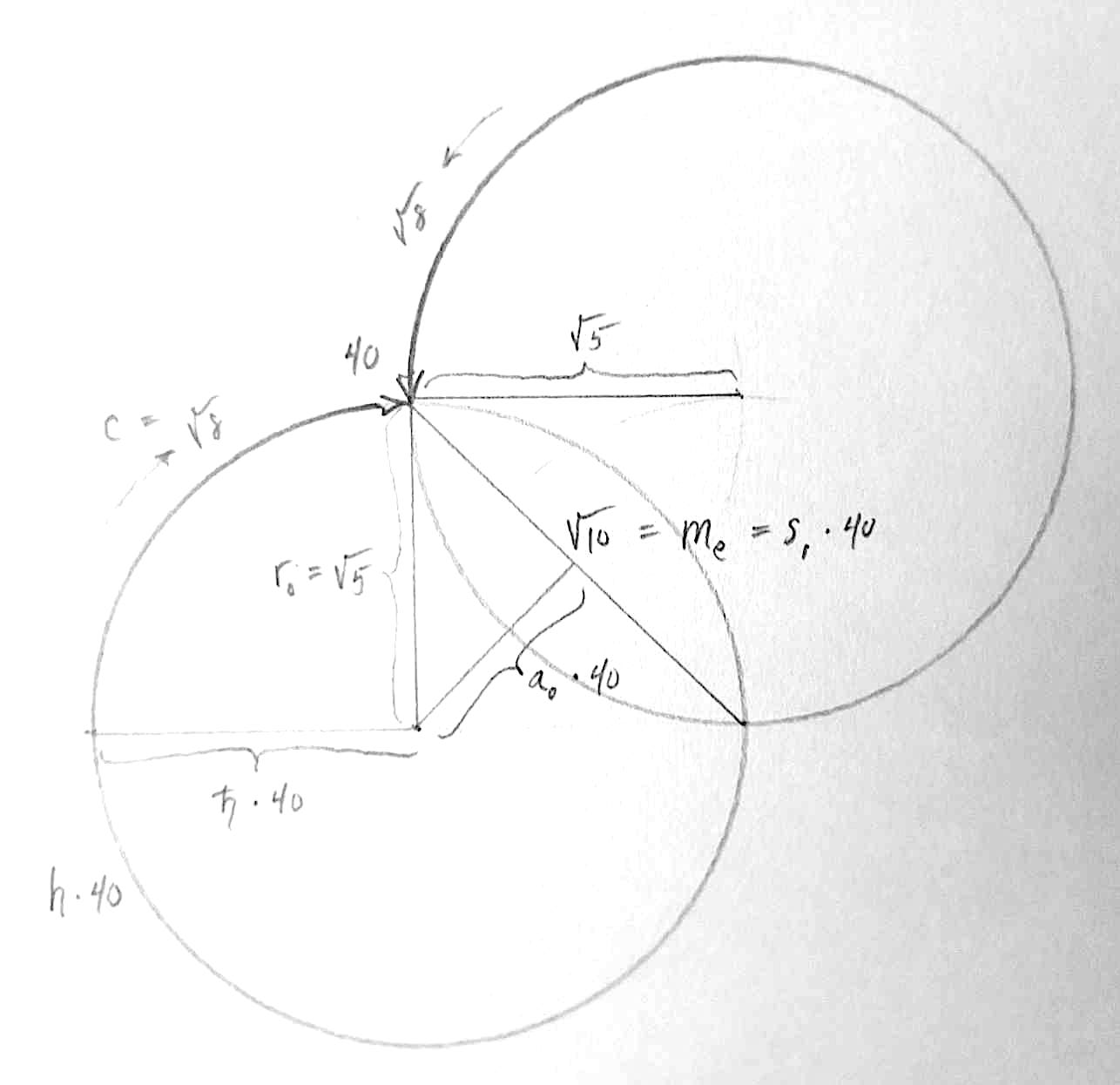
• √5 — rₒ — innermost stable circular orbit (the spatial radius)

• √8 — c — speed of light (the rate of circumferential spin)

from these we can derive a number of others and attempt to place them.

among them are:

• 5 — rₒ² — innermost stable circular orbit squared

• 8 — c² — speed of light squared

• 40 — λᵥᵥ— dimensionality of the node where circumferential spins merge

  • rₒ² * c² = 5 * 8 = 40

• √10 — mₑ — electron mass (one side of the projected diamond)

• π / √80 — h — planck’s constant (the circumference divided by 40)

• 1 / √320 — ℏ — reduced planck’s constant (the radius divided by 40)

• 1 / √160 — s₁ — 1 spin (side of the diamond divided by 40)

• 1 / √640 — a₀ — bohr radius (half the side of the diamond divided by 40)

  • this happens to be the inverse electron rest energy as well (1 / mₑc²)

• π — λᵣ — rydberg wavelength (circumference around a diameter of 1)

the following is known about particle spin values from real physics:

• s₁ₗ₂ — ℏ * √6 / √8 — 1/2 spin (particles with mass that take up space)

• s₁ — ℏ * √2 — 1 spin (photons, or light particles, mediating electromagnetism)

• s₂ — ℏ * √6 — 2 spin (the theoretical graviton, mediating gravity)

now also recall:

• 1 spin — ℏ * √2 — corresponds to one side of the diamond (divided by 40)

• c / √6, or √8 / √6 (given our assignment for c) is the speed requirement for massive particles to remain in orbit at rₒ (we told ourselves to remember this)

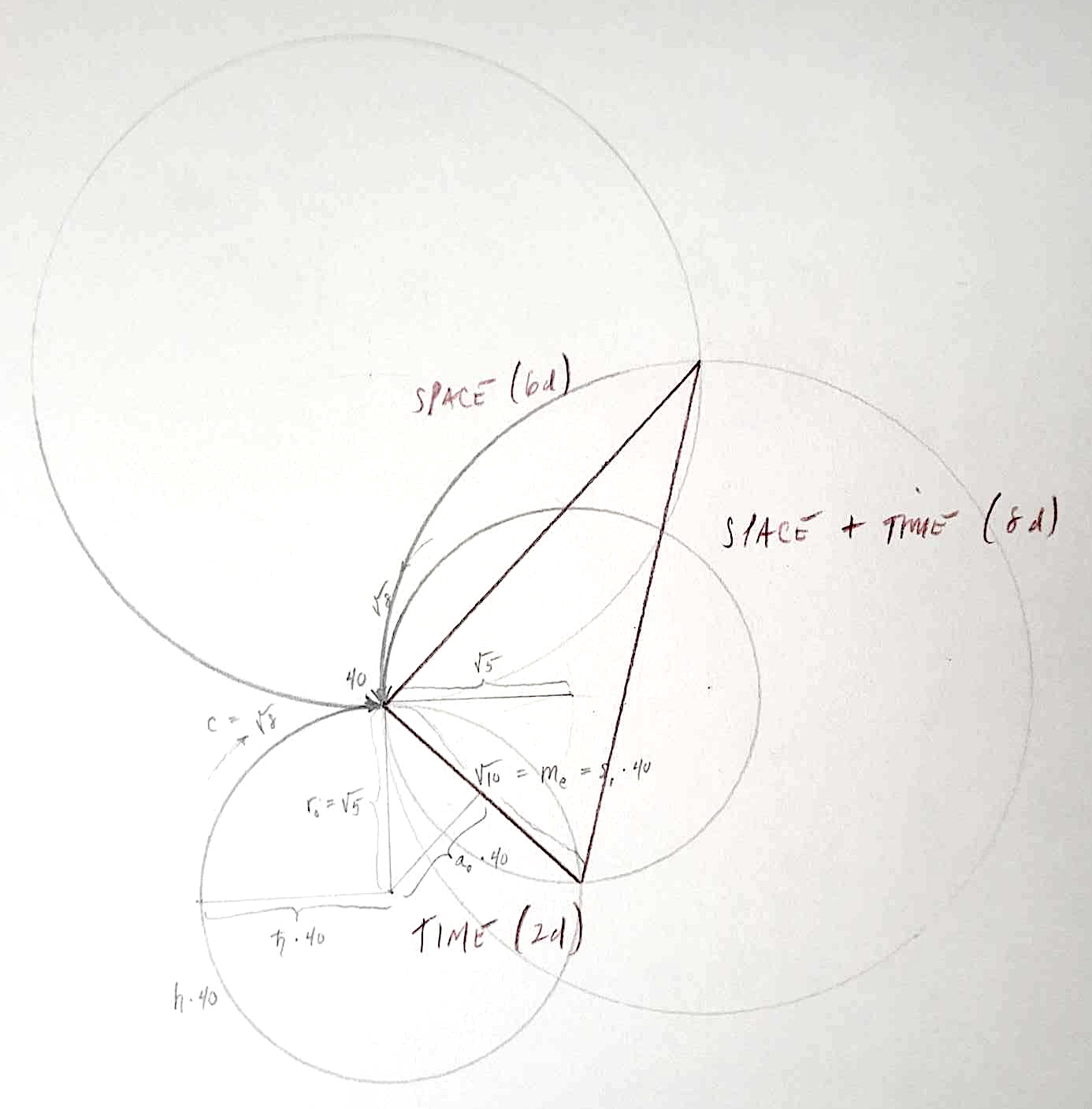
what we suspect is that instead of 2 circumferences spinning together, there are actually 8, with the two previously shown contributing to time, and 6 more contributing to space.

• the half spin particles (matter) spin in the 6 spatial dimensions, thereby remaining cohesive or bound within the 8 dimensional frame overall, subject to both time and space.

• the photons spin in time and freely escape into space.

• the opposite is true of the gravitons — they spin in space and maximally advance in time.

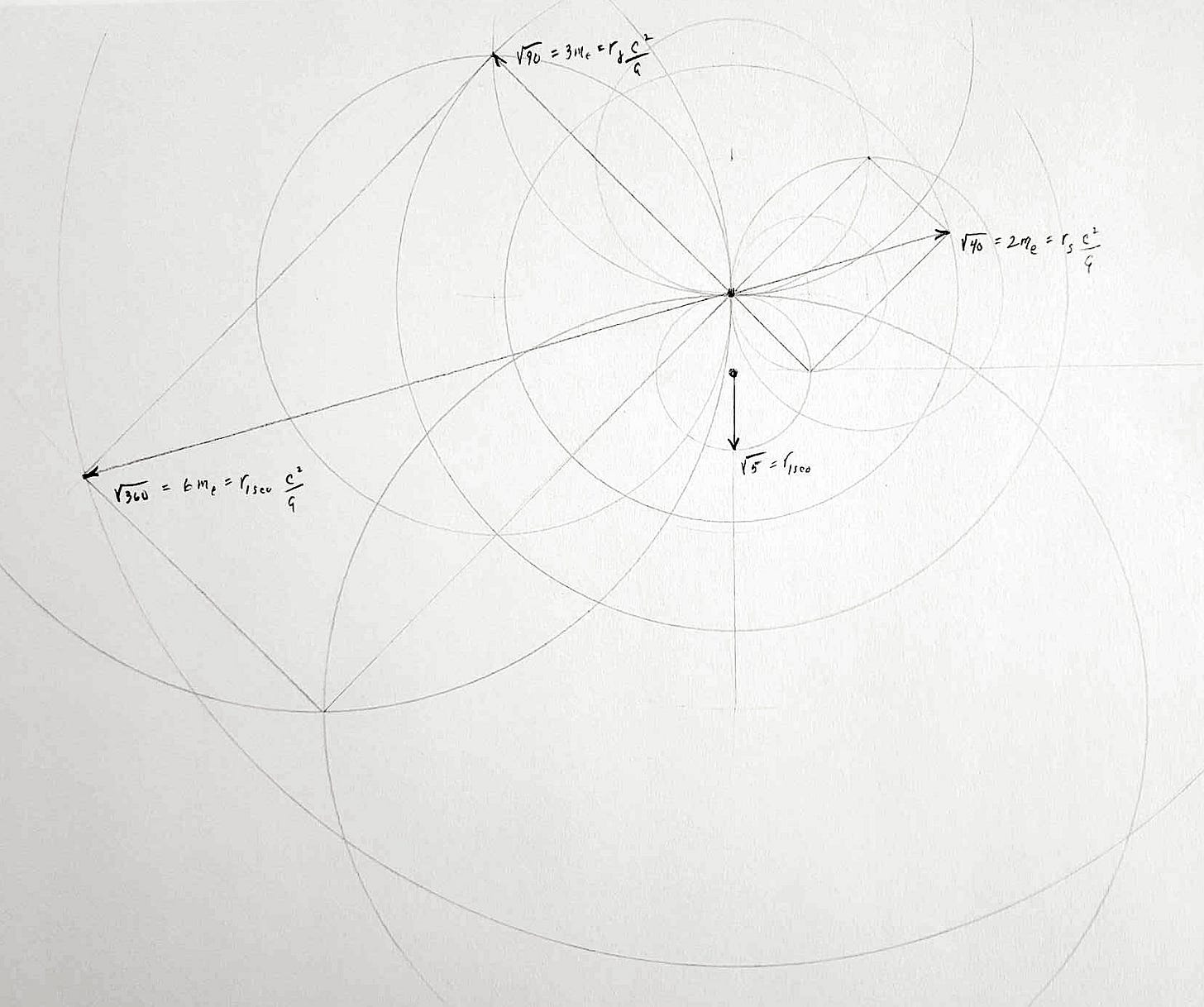
now lest we wonder what happens if matter isn’t obviously at the innermost stable circular orbit of a black hole, we’re suggesting that it always is. just a different one. same center, different circumference, different dimension however projected onto the 4 (or 8) we experience. this is possible at any scale (however quantized, obviously at small scales, less obviously so at large scales) because the model is fractal, by virtue of the 8 circumferences spinning into each other. remember, our speed of light at the outset was already √8 for inbound spins. this is why. 8 spinning circumferences push together to project √8 at a new scale, a level up.

in case we still wonder whether starting with √5 and √8 is a good idea, there is one more feature to this model worth mentioning. if we consider that in our diagram the diamond edge is oriented to the arrow of time, we have these ratios and their corresponding projections:

• 2 : 8 — √2 / √8 — the ratio of the overlaid spinning circumferences

• mₑ : c — √10 / √8 — the length of the diamond side relative to the speed of light circling over it

which, added together:

• Φ = √2 / √8 + √10 / √8 — the golden ratio

the thought is that the self-similarity inherent in the golden ratio at all scales — as above, so below — is what lends to this pattern arising from the noise to become the standing wave that is the manifest universe. not to mention, this seems to suggest a direct relationship between the curvature of space relative to any mass, and the speed of light is the same in all frames, so please consider it a challenge to adapt einstein’s field equations to this model :) in fact, please take it further and prove the fundamental relationship between the speed of light and the innermost stable circular orbiting radius around the one true black hole. our starting point, as it were.

appendix:

1. c = √8 — speed of light

2. rₒ = √5 — innermost stable circular orbit

3. λᵥᵥ = 40 — wishdrops wavelength (color spectrum root), ~1160 nm

4. Fₑd² = 1 / 40 — electric unit force times distance squared

5. mₑ = √10 — electron mass

6. mₑc² = √640 — electron rest energy

7. a₀ = 1 / √640 — Bohr radius

8. 2πa₀ = π / √160 — Bohr circumference

9. h = π / √80 — Planck’s constant

10. ℏ = 1 / √320 — reduced Planck’s constant

11. R = 1 / π — Rydberg constant

12. λᵣ = π — Rydberg wavelength

13. vᵣ = c * w₀ / 40 — √8 / π — Rydberg frequency

14. Ry = 1 / √10 — Rydberg energy

15. α = 1 / √40 — fine structure constant

16. w₀ = 40 / π — wishdrops ratio

17. c² = 1 / ε₀ / μ₀ — Maxwell’s relationship

18. ε₀ = e² / 2 / α / c / h — electric constant definition

19. Ry = mₑ * e⁴ / 8 / ε₀² / h² — Rydberg energy definition

20. a₀ = 4π * ε₀ * ℏ² / mₑ / e² — Bohr radius definition

21. α = e² / 4π / ε₀ / ℏ / c — fine structure constant definition

22. 4πk = 1 / ε₀ — electric constant identity

23. 4πa₀ = α * λᵣ — Bohr circumference identity

24. Ry = R * h * c — Rydberg energy relationship to Rydberg constant

25. e = √9 / w₀ — electric charge

26. ε₀ = 9π / 160 — permittivity of free space (electric constant)

27. μ₀ = 20 / 9π — permeability of free space (magnetic constant)

28. Z₀ = √(μ₀ / ε₀) = √2 * 40 / 9π — impedance of free space

29. k = 40 / 9π² — Coulomb’s constant

30. rγ = √5 / √4 — photon sphere radius

31. rₛ — √5 / √9 — schwarzschild radius (event horizon)

32. G — √8 / √9 — gravitational constant

33. rₑ = 1 / 320 / √10 — classical electron radius

34. rq = 1 / 160 — magnetic moment of the electron radius

35. α = rₑ / rq — electron radius to magnetic moment of electron radius

36. 1 / α = mₑ⁴c⁴ * rₑ — fine structure correlation to classical electron radius

37. 1 / α² = mₑ⁴c⁴ * rq — fine structure correlation to magnetic moment of electron radius

38. α * h = e² — fine structure, Planck’s constant, and electric charge

39. α² / e² = k — fine structure, electric charge, and Coulomb’s constant

40. α² = Fₑ * d² — fine structure, electric force and distance

41. α = F_mp * d² — fine structure, Planck mass force and distance

42. α = Fₑ / F_mp — fine structure, electric force and Planck mass force

43. pγᵣ = Ry / c = R * h = 1 / √80 — momentum of a photon with Rydberg energy

44. p_l = ℏ / a₀ = mₑ * c * α = √2 — linear momentum of a ground state electron in the Bohr model

45. Eλ = Ry / w₀ = 1 / √10 / w₀ — wishdrops energy

46. eV ~= Eλ * √7 / √8 — √7 / √80 / w₀ — one electron volt (approximately)

47. λ(#) = λᵥᵥ / √# — pure color wavelengths

    1. λ(1) = λᵥᵥ / √1 = ~1160 nm — wishdrops wavelength

    2. λ(2) = λᵥᵥ / √2 = ~820 nm — infrared onset

    3. λ(3) = λᵥᵥ / √3 = ~670 nm — red

    4. λ(4) = λᵥᵥ / √4 = ~580 nm — yellow

    5. λ(5) = λᵥᵥ / √5 = ~519 nm — green

    6. λ(6) = λᵥᵥ / √6 = ~474 nm — blue

    7. λ(7) = λᵥᵥ / √7 = ~438 nm — indigo

    8. λ(8) = λᵥᵥ / √8 = ~410 nm — violet 2³

    9. λ(9) = λᵥᵥ / √9 = ~387 nm — violet 3²

    10. λ(10) = λᵥᵥ / √10 = ~367 nm — uv onset

48. vᵥᵥ = vᵣ / w₀ — c / 40 — wishdrops frequency (color spectrum root)

    1. 3290 Thz / √162 = ~258 Thz

49. v(#) = vᵥᵥ * √# — pure color frequencies

    1. v(1) = vᵥᵥ * √1 = ~258 Thz — wishdrops frequency

    2. v(2) = vᵥᵥ * √2 = ~366 Thz — infrared onset

    3. v(3) = vᵥᵥ * √3 = ~448 Thz — red

    4. v(4) = vᵥᵥ * √4 = ~517 Thz — yellow

    5. v(5) = vᵥᵥ * √5 = ~578 Thz — green

    6. v(6) = vᵥᵥ * √6 = ~633 Thz — blue

    7. v(7) = vᵥᵥ * √7 = ~684 Thz — indigo

    8. v(8) = vᵥᵥ * √8 = ~731 Thz — violet 2³

    9. v(9) = vᵥᵥ * √9 = ~775 Thz — violet 3²

    10. v(10) = vᵥᵥ * √10 = ~817 Thz — ultraviolet onset

50. vᵤᵥ = v(10) = vᵥᵥ * √10 — c / √160 — ultraviolet onset frequency

51. d(480) = (√8 / √9) ^ 480 — weak force coupling constant (~5e-13)

52. d(1600) = (√8 / √9) ^ 1600 — gravitational coupling constant (~1e-41)

53. vₒ = vᵥᵥ * d(480) = ~136 hz — om frequency

    1. forty octaves below wishdrops frequency

54. vᵤ = vᵤᵥ * d(480) = ~432 hz — frequency of the universe (auditory spectrum center)

    1. forty octaves below ultraviolet onset frequency

addendum: